Dimo's Quest
Password generator
Function: Calculates Dimo's Quest level passwords from samples
Written by CD-i Fan <cdifan@gmail.com>
PHP version written by Shikotei Hikushi
The Dimo's Quest CD-i title issues level passwords after each completed level. By entering this password, the user can start directly at the next level.
The list of passwords is different for each CD-i player, because it is generated from a 32-bit random number stored in the first four bytes of the NVRAM file "Dimos_quest". When this file is first created the random number is generated based on the current time, which in practice means that it is unique for each CD-i player.
If the CD-i player has an empty NVRAM battery, all NVRAM contents will be lost each time the player loses power. The effect is that all previously issued level passwords become useless.
The level password generation algorithm leaks enough information that a few passwords are enough to uniquely determine the random number and thus the full set of generated level passwords. In practice it seems that three full passwords are exactly enough to uniquely determine the full set.
What this means is that after losing NVRAM, the user can just play the first three levels (which are easy) and then use this program to generate the full level password set. By entering the appropriate level password, any level can then be reached.
Each password has 8 characters, consisting of 4 consonant-vowel pairs. Dimo's Quest generates the 50 * 8 = 400 characters of these passwords as a single run of 200 pairs.
Each pair is generated from 8 bits of a 16-bit random number half, which means that it determines some possible values for those 8 bits. The generation algorithm used implies that each pair determines from 1 to 4 possible values for those bits.
The random number iteration algorithm uses a 32-bit random number, but 16 bits of these are always equal to the other 16 bits of the 32-bit random number from the previous iteration.
This means that the first two pairs determine from 1 to 16 possible values for 16 bits of the 32-bit random number. The remaining number of values is at most 16 * 2^16 = 2^20 which is small enough that just iterating over those and matching the generated pairs against the specified pairs is fast enough to be feasible.
There are (20 * 6) ^ 4 = 207,360,000 or about 2E8 different passwords. Since three full passwords seem to uniquely determine the full set, this means that there are about 8E24 or 8 quadrillion different sets.
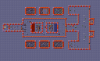
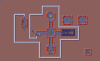
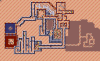
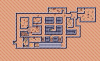
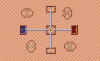
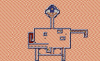
Level designs
Each of these maps are created from the on-disc tileset and level codes.
The switches information is in a format I haven't been able to determine. Otherwise I would have added the alternative designs per switch.
Dimo still looks like a frog (like in the original Amiga version) because that is how it is stored in the tileset data.
There are tons of texts in the designs that are beyond the viewing of the player.
The beige color in many of the tiles are supposed to be 'abyss', but I haven't found the abyss animations. I did make them transparent. Some of these tiles are ice cubes (rocks) that sit on top of an item like a key, candy, or bomb.